三维线段多平面重建
科研之路开始的地方~
问题表达
线段表示(两端点)
\[l=\mathbf{p}_1:(x_1,y_1,z_1)\rightarrow \mathbf{p}_2:(x_2,y_2,z_2)\]平面表示(点法式)
\[f=\{\mathbf{v}:(a,b,c),\mathbf{n}:(n_x,n_y,n_z)\}\]对于给定三维线段集$D={l_1,l_2,\cdots,l_n}$,如何重建出平面集${f_1,f_2,\cdots,f_k}$,$k$未知,使得线段到所属平面距离最小。作为聚类问题来处理。
概率建模
假设平面的数量$k$已知,同时假设各个面的概率分布为: $\mathrm{P}(f_1),\mathrm{P}(f_2),\cdots,\mathrm{P}(f_k),\sum_{i=1}^k\mathrm{P}(f_i)=1$,接下来对条件概率$\mathrm{P}(l\,|f_i)$作出如下假设:
\[\mathrm{P}(l\,| f_i)=\frac1{\sqrt{2\pi}\sigma_i}\exp\{-\frac{[(\mathbf{p}_1-\mathbf{v}_i)\cdot \mathbf{n}_i]^2+[(\mathbf{p}_2-\mathbf{v}_i)\cdot \mathbf{n}_i]^2}{2\sigma_i^2}\}\]利用贝叶斯公式,可以得到线段样本的概率:
\[\mathrm{P}(l)=\sum_{i=1}^k\mathrm{P}(l\,|f_i)\mathrm{P}(f_i)\]对于目前给定的三维线段集$D={l_1,l_2,\cdots,l_n}$, 假设其中每个元素都是独立的样本,采样最大似然估计来估计上面模型的各个参数。假设以上平面和先验概率分布参数集合为$\theta$,接下来就是估计一个$\hat \theta$ 使得 $\mathrm{P}(D|\theta)$最大。
参数估计
考虑对数似然,
\[\ln[\mathrm{P}(D|\theta)]=\sum_{i=1}^n\ln[\mathrm{P}(l_i|\theta)]=\sum_{i=1}^n\ln[\sum_{j=1}^k\mathrm{P}(l_i|f_j,\theta_j)\mathrm{P}(f_j)]\]转化为优化问题求取参数。类似于高斯混合模型,采用EM算法来进行参数估计。
- 明确隐变量
反映观测线段$l_i$来自平面$f_j$的数据是未知的,用隐变量$\gamma_{ij}$表示,定义如下:
\[\gamma_{ij}= \begin{cases} \begin{aligned} 1,& \quad l_i\in f_j\\ 0,& \quad otherwise \end{aligned} \end{cases}\]那么可以写出完全数据的似然函数:
\[\begin{align} \mathrm{P}(l,\gamma|\theta)=& \prod_{i=1}^n\mathrm{P}(l_i,\gamma_{i1},\gamma_{i2},\ldots,\gamma_{ik}|\theta)\\=& \prod_{i=1}^n\prod_{j=1}^k\left[\mathrm{P}(l_i|f_j,\theta_j)\mathrm{P}(f_j)\right]^{\gamma_{ij}}\\=& \prod_{j=1}^k\mathrm{P}(f_j)^{c_j}\prod_{i=1}^n\left[\mathrm{P}(l_i|f_j,\theta_j)\right]^{\gamma_{ij}}\\=& \prod_{j=1}^k\mathrm{P}(f_j)^{c_j}\prod_{i=1}^n\left[\frac1{\sqrt{2\pi}\sigma_j}\exp\left({-\frac{((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2}{2\sigma_j^2}}\right)\right]^{\gamma_{ij}} \end{align}\]这里$c_j=\sum_{i=1}^n\gamma_{ij}$,完全数据的对数似然函数为
\[\ln\mathrm{P}(l,\gamma|\theta)=\sum_{j=1}^k\left\{c_j\ln \mathrm{P}(f_j)+\sum_{i=1}^n\gamma_{ij}\left[\ln\frac{1}{\sqrt{2\pi}\sigma_j}-\frac1{2\sigma_j^2}\left(((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2\right)\right] \right\}\]- 确定Q函数
EM算法的E的步骤,确定Q函数
\[\begin{gathered} \mathrm{Q}(\theta,\theta^{(i)})=\mathcal{E}[\ln\mathrm{P}(l,\gamma|\theta)|l,\theta^{(i)}]=\mathcal{E}\left\{\sum_{j=1}^k\left\{c_j\ln P(f_j)+\sum_{i=1}^n\gamma_{ij}\left[\ln\frac1{\sqrt{2\pi}\sigma_j}-\frac{((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2}{2\sigma_j^2}\right]\right\}\right\} =\sum_{j=1}^k\left\{\sum_{i=1}^n\mathcal{E}(\gamma_{ij})\ln P(f_j)+\sum_{i=1}^n\mathcal{E}(\gamma_{ij})\left[\ln\frac1{\sqrt{2\pi}\sigma_j}-\frac{((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2}{2\sigma_j^2}\right]\right\} \end{gathered}\]计算期望$\mathcal{E}(\gamma_{ij}|l_i,\theta)$, 记为$\hat\gamma_{ij}$:
\[\begin{align} \hat\gamma_{ij}=&\mathcal{E}(\gamma_{ij}|l_i,\theta)=P(\gamma_{ij}=1|l_i,\theta_j)\\ =&\frac{P(\gamma_{ij}=1,l_i|\theta_j)}{\sum_{j=1}^kP(\gamma_{ij}=1,l_i|\theta_j)}\\=& \frac{P(l_i|\gamma_{ij}=1,\theta_j)P(\gamma_{ij}=1|\theta)}{\sum_{j=1}^kP(l_i|\gamma_{ij}=1,\theta_j)P(\gamma_{ij}=1|\theta)}\\=& \frac{P(f_j)P(l_i|f_j,\theta)}{\sum_{j=1}^kP(f_j)P(l_i|f_j,\theta)} \end{align}\]将$\hat \gamma_{ij},c_j=\sum_{i=1}^n\hat \gamma_{ij}$代入Q函数得到
\[\mathrm{Q}(\theta,\theta^{(i)})=\sum_{j=1}^kc_j\ln P(f_j)+\sum_{i=1}^n\hat \gamma_{ij}\left[\ln\frac1{\sqrt{2\pi}\sigma_j}-\frac{((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2}{2\sigma_j^2}\right]\]- 求极大
因为$\sum_{i=1}^k\mathrm{P}(f_i)=1$约束最优化问题可以写成
\[\max_{\theta}\,\mathrm{Q}(\theta,\theta^{(i)})\\ \begin{align} s.t. \sum_{j=1}^k\mathrm{P}(f_j)=1 \end{align}\]写成拉格朗日函数:
\[\mathcal{L}=\mathrm{Q}(\theta,\theta^{(i)})+\lambda\left[1-\sum_{j=1}^k\mathrm{P}(f_j)\right]\]对$P(f_j)$求偏导并令其为0:
\[\frac{\partial\mathcal{L}}{\partial P(f_j)}=\frac{c_j}{P(f_j)}-\lambda=0\Rightarrow c_j=\lambda P(f_j)\Rightarrow \sum_{j=1}^n c_j=\sum_{j=1}^n \lambda P(f_j)\Rightarrow \lambda=n\Rightarrow P(f_j)=\frac{c_j}{n}\]对$\sigma_j$求偏导并令其为0:
\[\frac{\partial \mathcal{L}}{\partial \sigma_j}=\sum_{i=1}^n \hat\gamma_{ij}\frac{((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2-\sigma_j^2}{\sigma_j^3}=0\\ \Downarrow\\ \sigma_j^2=\frac{\sum_{i=1}^n \hat\gamma_{ij}[((\mathbf{p}_{i1}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2+((\mathbf{p}_{i2}-\mathbf{v}_j)\cdot \mathbf{n}_j)^2]}{\sum_{i=1}^n \hat\gamma_{ij}}\]对$\mathbf{n}_j$求偏导并令其为0:
\[\frac{\partial\mathcal{L}}{\partial \mathbf{n}_j}= -\sum_{i=1}^n\frac{\hat \gamma_{ij}}{\sigma_j^2}[(\mathbf{p}_{i1}-\mathbf{v}_j)^T \mathbf{n}_j(\mathbf{p}_{i1}-\mathbf{v}_j)+(\mathbf{p}_{i2}-\mathbf{v}_j)^T \mathbf{n}_j(\mathbf{p}_{i2}-\mathbf{v}_j)]=0\\ \Downarrow\\ -\frac1{\sigma_j^2}\left\{\sum_{i=1}^n\hat\gamma_{ij}\left[(\mathbf{p}_{i1}-\mathbf{v}_j)(\mathbf{p}_{i1}-\mathbf{v}_j)^T +(\mathbf{p}_{i2}-\mathbf{v}_j)(\mathbf{p}_{i2}-\mathbf{v}_j)^T \right]\right\}\mathbf{n}_j=0\]令
\[A=\left\{\sum_{i=1}^n\hat\gamma_{ij}\left[(\mathbf{p}_{i1}-\mathbf{v}_j)(\mathbf{p}_{i1}-\mathbf{v}_j)^T +(\mathbf{p}_{i2}-\mathbf{v}_j)(\mathbf{p}_{i2}-\mathbf{v}_j)^T \right]\right\}\]解线性方程$A\mathbf{n}_j=0$得到$\mathbf{n}_j$,但是该方程不一定有非零解。考虑到这一点,将该问题再转化为优化的问题
\[\min_{\mathbf{n}_j}\Vert A\mathbf{n}_j\Vert\]因为尺度大小的影响,对$\mathbf{n}_j$再加入一个约束$\Vert\mathbf{n}_j\Vert=1$,可以得到
\[\min_{\mathbf{n}_j} \mathbf{n}_j^TA^TA\mathbf{n}_j\\ \begin{align} s.t. \mathbf{n}_j^T\mathbf{n}_j=1 \end{align}\]等价于对$A^TA$进行特征值分解,因为$A^TA$半正定,而且$A$是半正定对称矩阵,所以$A$最小特征值对应的特征向量即为$\mathbf{n}_j$;
对$\mathbf{v}_j$求偏导并令其为0
\[\frac{\partial\mathcal{L}}{\partial \mathbf{v}_j}=\sum_{i=1}^n\frac{\hat \gamma_{ij}}{\sigma_j^2}[\mathbf{n}_j^T(\mathbf{p}_{i1}-\mathbf{v}_j)\mathbf{n}_j+\mathbf{n}_j^T(\mathbf{p}_{i2}-\mathbf{v}_j)\mathbf{n}_j]=0\\ \Downarrow\\ \frac1{\sigma_j^2}\sum_{i=1}^n\hat\gamma_{ij}\left[\mathbf{n}_j\mathbf{n}_j^T(\mathbf{p}_{i1}+\mathbf{p}_{i2}-2\mathbf{v}_j)\right]=0\\ \Downarrow\\ \frac1{\sigma_j^2}\mathbf{n}_j\mathbf{n}_j^T\left[\sum_{i=1}^n\hat\gamma_{ij}(\mathbf{p}_{i1}+\mathbf{p}_{i2})\right]=\frac2{\sigma_j^2}\mathbf{n}_j\mathbf{n}_j^T\left(\sum_{i=1}^n\hat\gamma_{ij}\right)\mathbf{v}_j\\ \Downarrow\\ \mathbf{v}_j=\frac{\sum_{i=1}^n\hat\gamma_{ij}(\mathbf{p}_{i1}+\mathbf{p}_{i2})}{2\sum_{i=1}^n\hat\gamma_{ij}}\]算法描述
输入:三维线段集$D={l_1,l_2,\cdots,l_n}$,概率模型
输出:概率模型参数
-
取参数的初值开始迭代
-
E步:依据当前模型参数,计算平面对线段的响应度
- M步:计算新一轮迭代的模型参数,
- 重复2、3步直到收敛。
根据最终的$\mathbf{v}_j,\mathbf{n}_j(j=1,2,\ldots,k)$即可确定最后的平面集合。
TODO
类似于GMM到K-Means的简化,算法简化假设先验概率相等,后验概率0-1近似。和K-Means一样,模型对初值敏感,对outlier敏感。目前初值是选取模型包围盒对角线上的n点,每个点三个互相正交的平面。方差初始值设为两个面之间的距离
Results
cluster/3, iteration times
(11,22) 先进院部分面采样

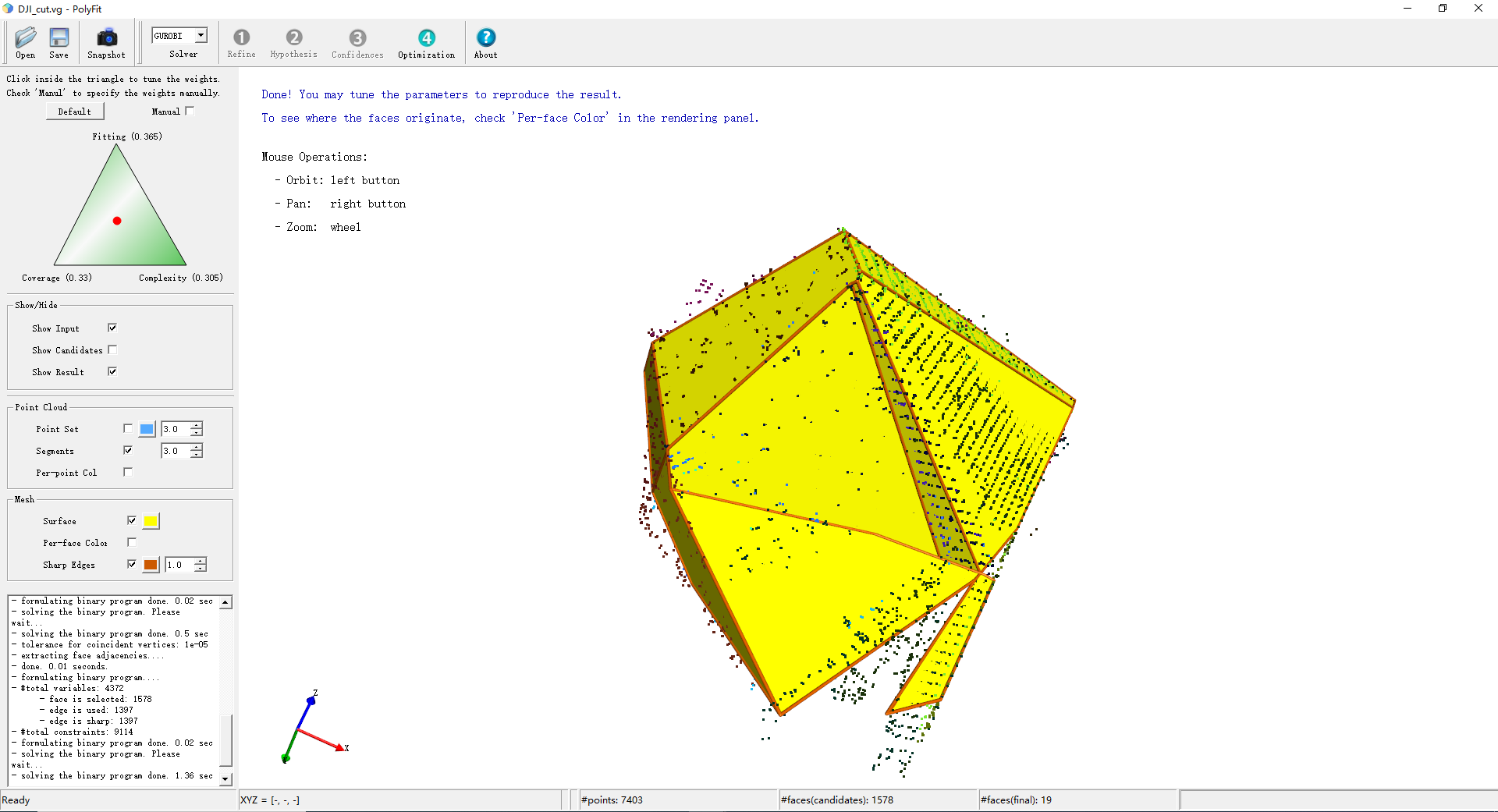
(19,25)大疆旗舰店

(15,30)先进院

(19)
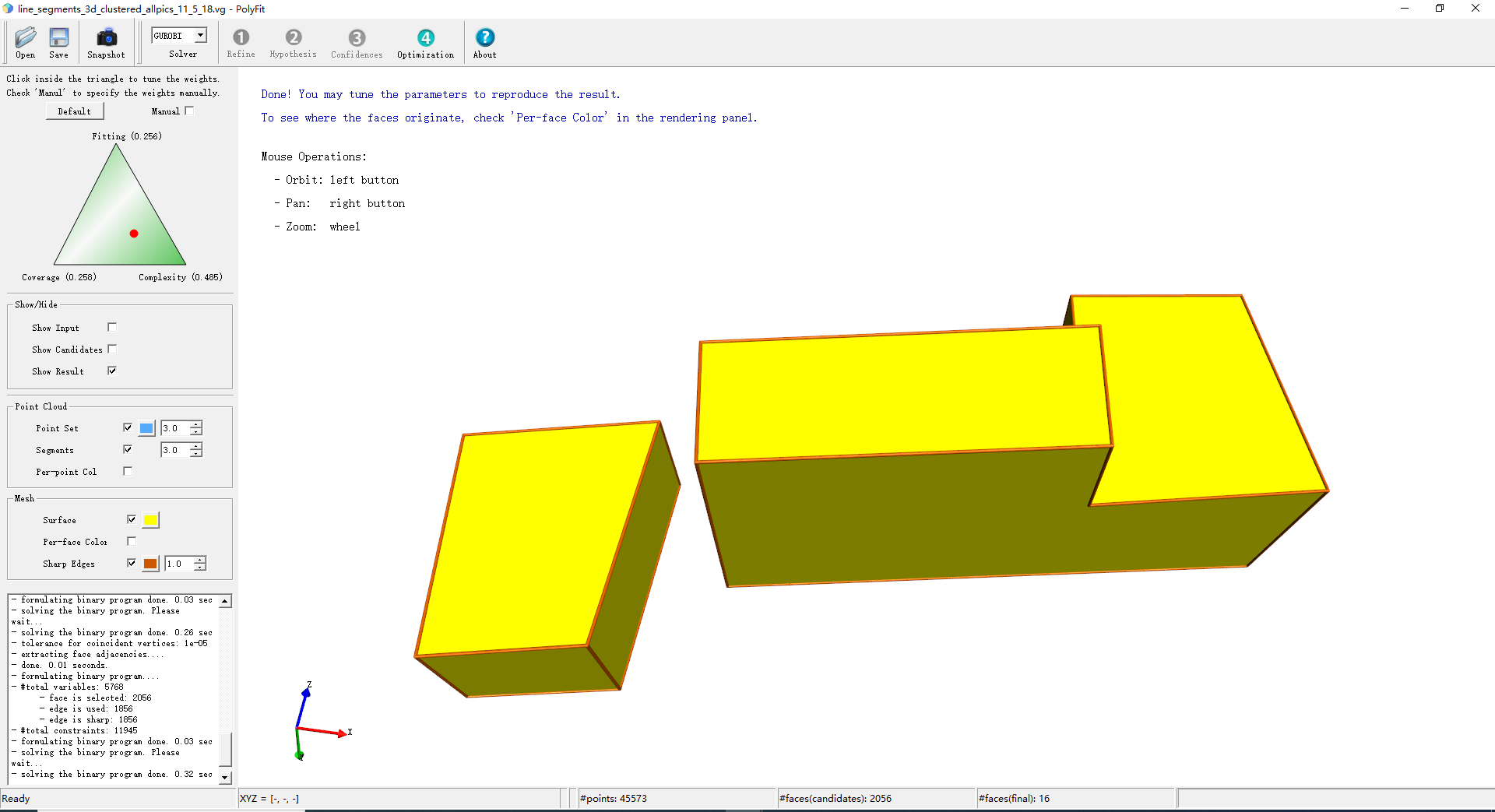
(41,56)
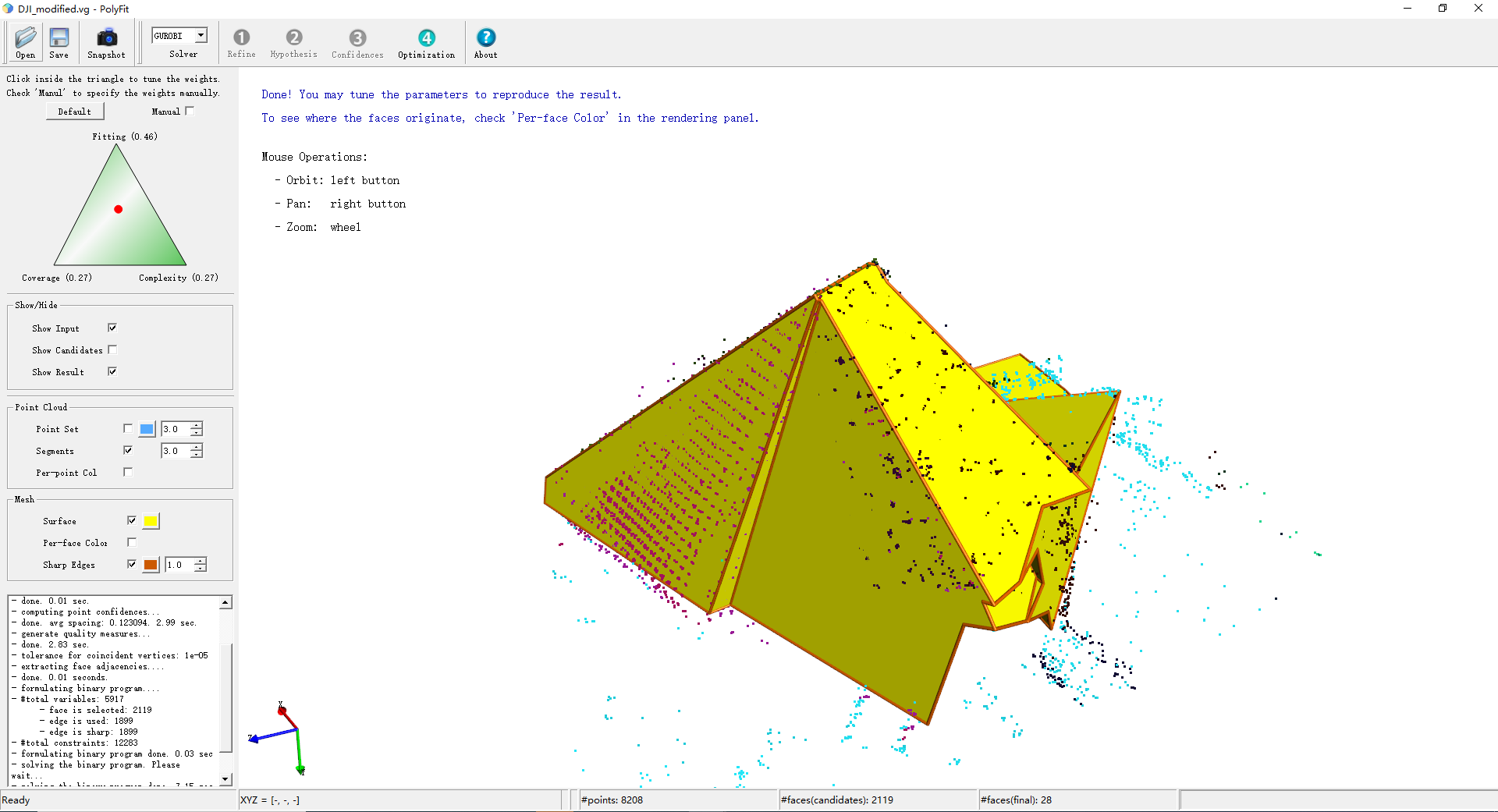
(41,50)大疆modified
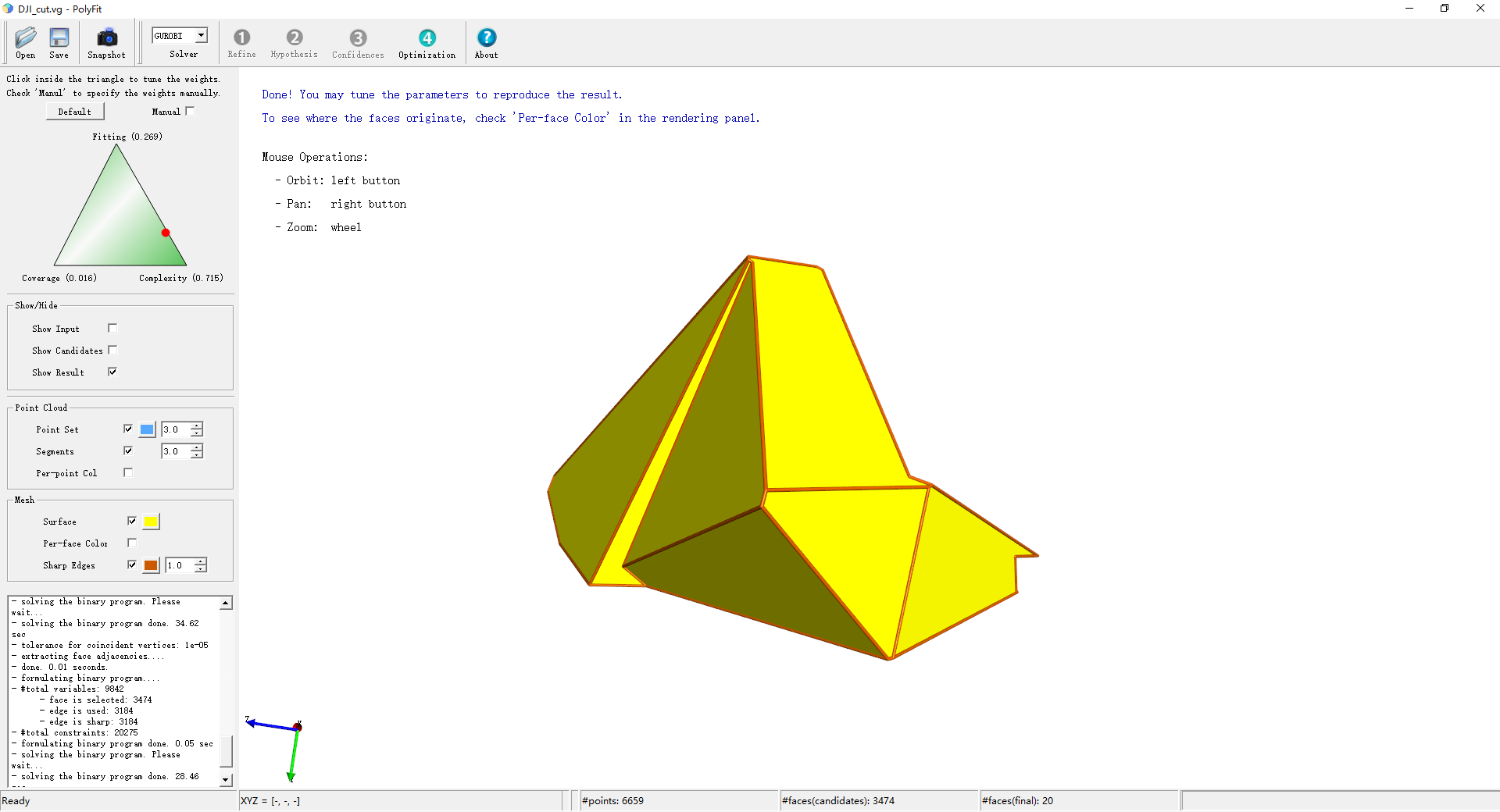
(53,49)
(61)
| 微信(WeChat Pay) | 支付宝(AliPay) |

|

|